Математика в Древней Индии
Category: Outro
Atualizado: 30 jan 2022
Autores

Created byСветлана Мугаллимова
Attachments
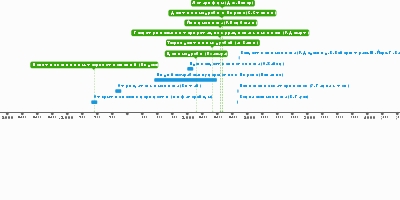
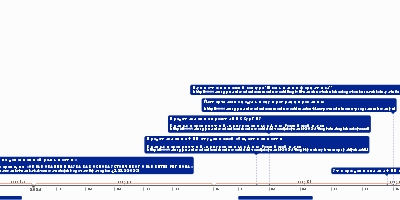
Eventos
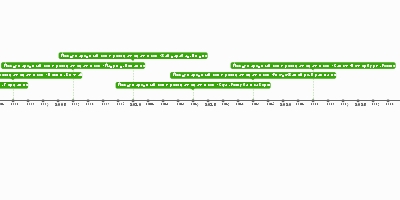
Сульба Сутра , ведический санскритский геометрический текст,
содержит квадратные уравнения
и вычисляет квадратный корень из двух с точностью до пяти десятичных знаковЯджнавалкья описывает движения солнца и луны
и продвигает 95-летний цикл, чтобы синхронизировать движения солнце и луныЯджурведа , одна из четырех индуистских Вед ,
содержит самую раннюю концепцию бесконечностиСурья Праджинапти, математический текст,
в котором все числа классифицируются по трем группам:
перечислимым, бесчисленным и бесконечнымИндийские тексты используют санскритское слово «Шунья»
для обозначения понятия «пустота» (ноль )Пингала пишет Чханда-шастру,
которая содержит первое индийское использование нуля в качестве цифры;
представляет описание двоичной системы счисления,
наряду с первым использованием чисел Фибоначчи и треугольника ПаскаляСтхананга-сутра содержит работы по теории чисел,
арифметическим операциям, геометрии,операциям с дробями,
простым уравнениям, кубическим уравнениям, уравнениям четвертой степени,
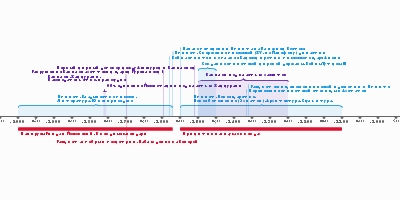
перестановкам и комбинациямПервая позиционная запись в десятеричной системе счисленияЛагадха пишет Веданга Джйотиша, ведический текст по астрономии ,
который описывает правила отслеживания движений Солнца и Луны ,
использует геометрию и тригонометрию для астрономииБахшалийская рукопись описывает теорию бесконечности,
содержащую различные уровни бесконечности, логарифмы с основанием 2,
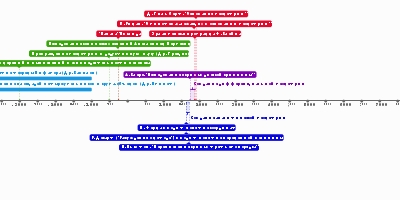
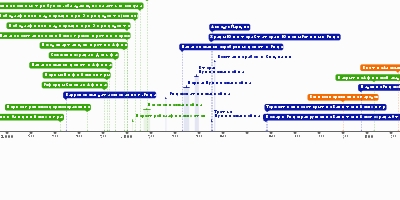
вычисляет квадратные корни из чисел размером до миллиона с точностью не менее 11 десятичных знаковАриабхата вводит тригонометрические функции и методы вычисления их приблизительных числовых значений,
определяет понятия синус и косинус, составляет таблицы значений синуса и косинусаЧисловое представление нуля в позиционной системе счисленияБхаскара I дает рациональную аппроксимацию функции синусаБрахмагупта предлагает метод решения неопределенных уравнений второй степени,
применяет алгебру для решения астрономических задачБрахмагупта дает правила для работыкак отрицательными, так и положительными числами,
методы вычисления квадратных корней, методы решения линейных и квадратных уравнений,
правила суммирования рядовВирасена дает правила для последовательности Фибоначчи,
вывод объема с использованием бесконечно малой величиныШридхара дает правило для определения объема сферы,
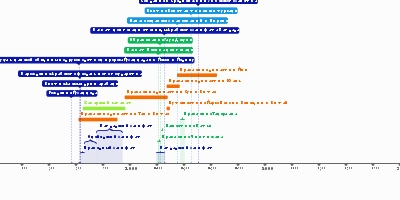
а также формулу для решения квадратных уравненийКанка привозит Брахма-спхута-сиддханту Брахмагупты в БагдадАль-Фазари переводит Брахма-спхута-сиддханту на арабский языкМахавира дает систематические правила
для выражения дроби как суммы единичных дробейБхаскара II Ачарья пишет"Лилавати"Бхаскара II задумывает дифференциальное исчисление,
доказывает теорему Пифагора, доказывает, что деление на ноль равно бесконечности,
вычисляет π с точностью до 5 знаков после запятой
и вычисляет время, необходимое Земле для обращения вокруг Солнца
с точностью до 9 знаков после запятойПарамешвара представляет последовательную форму
синусоидальной функции, которая эквивалентна ее разложению в ряд Тейлора,
утверждает теорему о среднем значении дифференциального исчисленияМадхава обнаруживает разложение в ряд для функции обратной тангенсу,
бесконечный ряд для arctan и sin, методы для вычисления длины окружности,
и использует их для вычисления π с точностью до 11 знаков после запятой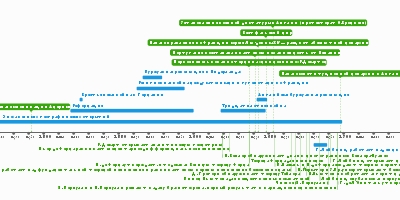







Comments